Heap Complexity
The part just shown very similar to removal from a heap which is O(log(n)). You do it n-1 times so it is O(nlog(n)). The last steps are cheaper but for the reverse reason from the building of the heap, most are log(n) so it is O(nlog(n)) overall for this part. The build part was O(n) so it does not dominate. For the whole heap sort you get O(nlog(n)).There is no extra memory except a few for local temporaries.
Thus, we have finally achieved a comparison sort that uses no extra memory and is O(nlog(n)) in the worst case.
In many cases people still use quick sort because it uses no extra memory and is usually O(nlog(n)). Quick sort runs faster than heap sort in practice. The worst case of O(n2) is not seen in practice.
Complexity Analysis of Bubble Sorting
In Bubble Sort, n-1 comparisons will be done in 1st pass, n-2 in 2nd pass, n-3 in 3rd pass and so on. So the total number of comparisons will be
(n-1)+(n-2)+(n-3)+.....+3+2+1
Sum = n(n-1)/2
i.e O(n2)
Hence the complexity of Bubble Sort is O(n2).The main advantage of Bubble Sort is the simplicity of the algorithm.Space complexity for Bubble Sort is O(1), because only single additional memory space is required for temp variable
Best-case Time Complexity will be O(n), it is when the list is already sorted.
We assume that we're sorting a total of
n elements in the entire array.- The divide step takes constant time, regardless of the subarray size. After all, the divide step just computes the midpoint
qof the indicespandr. Recall that in big-Θ notation, we indicate constant time byΘ(1). - The conquer step, where we recursively sort two subarrays of approximately
n/2elements each, takes some amount of time, but we'll account for that time when we consider the subproblems. - The combine step merges a total of
nelements, takingΘ(n)time.
If we think about the divide and combine steps together, the
Θ(1) running time for the divide step is a low-order term when compared with the Θ(n)running time of the combine step. So let's think of the divide and combine steps together as taking Θ(n) time. To make things more concrete, let's say that the divide and combine steps together take cn time for some constant c.Let's draw out the merging times in a "tree":
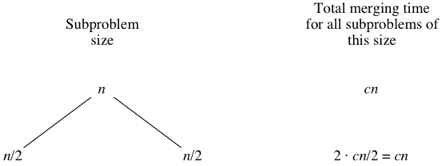
Computer scientists draw trees upside-down from how actual trees grow. Atree is a graph with no cycles (paths that start and end at the same place). Convention is to call the vertices in a tree its nodes. The root node is on top; here, the root is labeled with the
n subarray size for the original n-element array. Below the root are two child nodes, each labeled n/2 to represent the subarray sizes for the two subproblems of size n/2.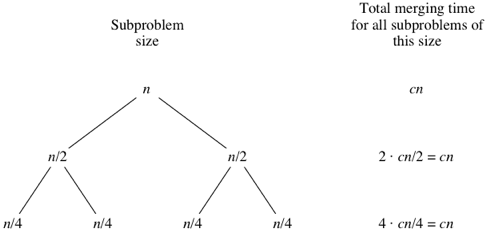
What do you think would happen for the subproblems of size
n/8? There will be eight of them, and the merging time for each will be cn/8, for a total merging time of 8⋅cn/8=cn: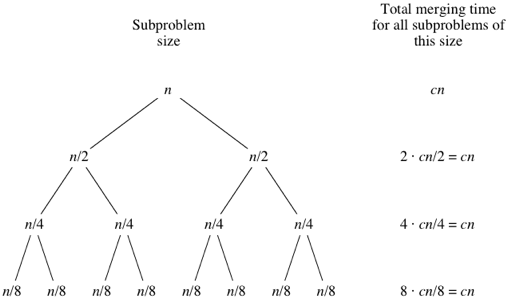
As the subproblems get smaller, the number of subproblems doubles at each "level" of the recursion, but the merging time halves. The doubling and halving cancel each other out, and so the total merging time is
cn at each level of recursion. Eventually, we get down to subproblems of size 1: the base case. We have to spend Θ(1) time to sort subarrays of size 1, because we have to test whether p<r, and this test takes time. How many subarrays of size 1 are there? Since we started with n elements, there must be n of them. Since each base case takes Θ(1) time, let's say that altogether, the base cases take cntime: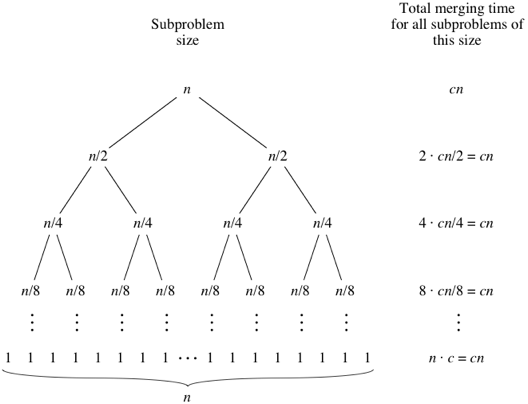
When we use big-Θ notation to describe this running time, we can discard the low-order term (
+1) and the constant coefficient (c), giving us a running time of Θ(nlgn), as promised.Read more from Source: https://www.khanacademy.org/computing/computer-science/algorithms/merge-sort/a/analysis-of-merge-sort





